成考高起专数学模拟题一（答案）

为更好备战2023年成人高考快师教育安徽成考网根据历年考试试题编写了模拟题及答案，并发布如下。由于题目都是自行整理而来的，故仅供广大考生参考，如有疑问或想要提供更多科目练习题的，可直接在线留言咨询。

1. B

本题主要考查的知识点为集合的运算。S、T都是函数的值域∵S={y|y=(1/2)2,x∈ R}⇒ S={ y|y >0}，T={y|y=x2-1，x∈R}⇒{ y|y≥-1}，∴ S∪T=T。

2. B

本题主要考查的知识点为简易逻辑。m≠ 0或n≠0⇒m2+n2≠0，m2+n2≠0⇒ m≠ 0或者n≠0。

3. C

4. D

本题主要考查的知识点为函数的定义域。选项A中x∈R且x≠ 0；选项B中x∈R且x≠ 0选项C中x∈R且x≠ kπ，k∈z；选项D中x∈R故应选D。

5. B

本题主要考查的知识点为指数函数的对称性。令x=t，把x=t代入y=3x得y=3t,把x=-t代入y=-3-x得-y=3t,易知函数y=3x与y=-3-x上任一点的横坐标互为相反数，纵坐标也互为相反数，∴函数y=3x与y=-3-x的图像关于原点对称。

6. A

本题主要考查的知识点为等比数列的性质。∵ {an} 是等比数列，∴若m+n=p+q，则am•an=ap•aq，∴a1•a2•a5•a6=（a3•a4）•（a3•a4）=25

7. D

8. A

9. A

本题主要考查的知识点为偶函数的性质。由f（x）为偶函数得f（-x）=f（x），∵a=f（log1/28）=f（-3）=f（3），b=f（-π）=f（π），3和π都属于[2，4]且3<π,∵f(x)在[2，4]上为减函数，∴ f（π）<f（3），∴a>b。

10. B

11. C

12. D

13. B

14. B

15. D

本题主要考查的知识点为两圆的位置关系。两圆的位置关系由两圆的圆心关系距d与两圆的半径和r1和r2的关系来判断，当d> r1+ r2的来判断，当d= r1+ r2时两圆外切；当|r1-r2|<d< r1+ r2时两圆相交；当d<|r1-r22+y2+16知该圆的圆心C1（0，0）,半径r1=4.由x2+y2-2x-3=0⇒(x-1)2+y2=4知该圆的圆心C2（1，0），半径r2=2. ∴ d=1<|4-2|=2∴两圆内含。

16. C

本题主要考查的知识点为曲线切线的倾斜角。由导致的几何意义可知曲线在某一点的切线的倾斜角的正切值就是曲线在这一点处的的导数值，即fˊ（x0）=tanα，∵ yˊ=2αx+1，∴ yˊ|x=0=1，∴tanα=1，∵ 0≤α<π，∴α=π/4。

17. B

本题主要考查的知识点为不等式的解集。|x+3|<5⇒-5<x+3<5⇒-8<x<2.

问答题

18. 

19. 

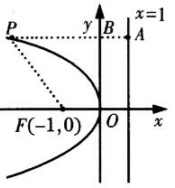
20. 答案：-3.本题主要考查的知识点为抛物线的性质。根据抛物线y2=4x画出图像，由抛物线的定义可帮助求解。由已知条件得焦点F(-1,0),准线方程x=1，由P点到焦点的距离|PF|=4得|PA|=4，∴|PB|=4-1=3，∴P点的横坐标为-3。

21. 

22. 

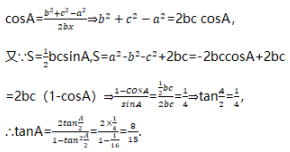
23. 利润L等于收入R减去成本Q，而收入等于产量乘以价格，由此得出利润L与产量的函数关系式再用导数求最大利润。收入R=P·m=P•（25-1/8·p2)=25P -1/8·p2利润L=R-Q=（25p-1/8·p2)-(100+4P)=-1/8·p2+21P-100,Lˊ=-1/4P+21,令Lˊ=0，得P=84，当P<84时，Lˊ>0,当P>0时，Lˊ<0，由此可知P=84时，L取最大值。故产量P为84时；利润L最大。

24. 

25.

更多推荐：

成考高起专数学模拟题一（试题）